Decoding Negative Image Distance: A Journey Through Optics and Digital Visuals at Tophinhanhdep.com

In the vast and intricate world of optics, understanding how light interacts with lenses and mirrors to form images is fundamental. From the simple act of looking at your reflection to the complex machinery of a high-resolution camera, the principles of image formation govern what we see. One particularly intriguing concept that often causes initial confusion is “negative image distance.” What exactly does it signify, and why is it crucial for both aspiring physicists and modern visual creators? At Tophinhanhdep.com, where we celebrate the richness of visual content—from breathtaking wallpapers and aesthetic backgrounds to inspiring digital art and powerful photography—the underlying principles of how images are formed, whether real or virtual, deeply resonate with our mission to provide diverse and high-quality visuals.

Negative image distance is not merely an abstract mathematical result; it’s a key indicator of a specific type of image: the virtual image. Unlike real images, which can be projected onto a screen, virtual images cannot. They exist where light rays only appear to converge or diverge from, rather than actually doing so. This concept, born from the rigorous application of sign conventions in geometrical optics, holds immense importance, not only in academic physics but also in understanding the art of perception, photography, and digital image creation. Join us as we explore the meaning behind negative image distance, delve into the optical principles that define it, and draw parallels to the fascinating world of digital images and visual design that Tophinhanhdep.com proudly curates.

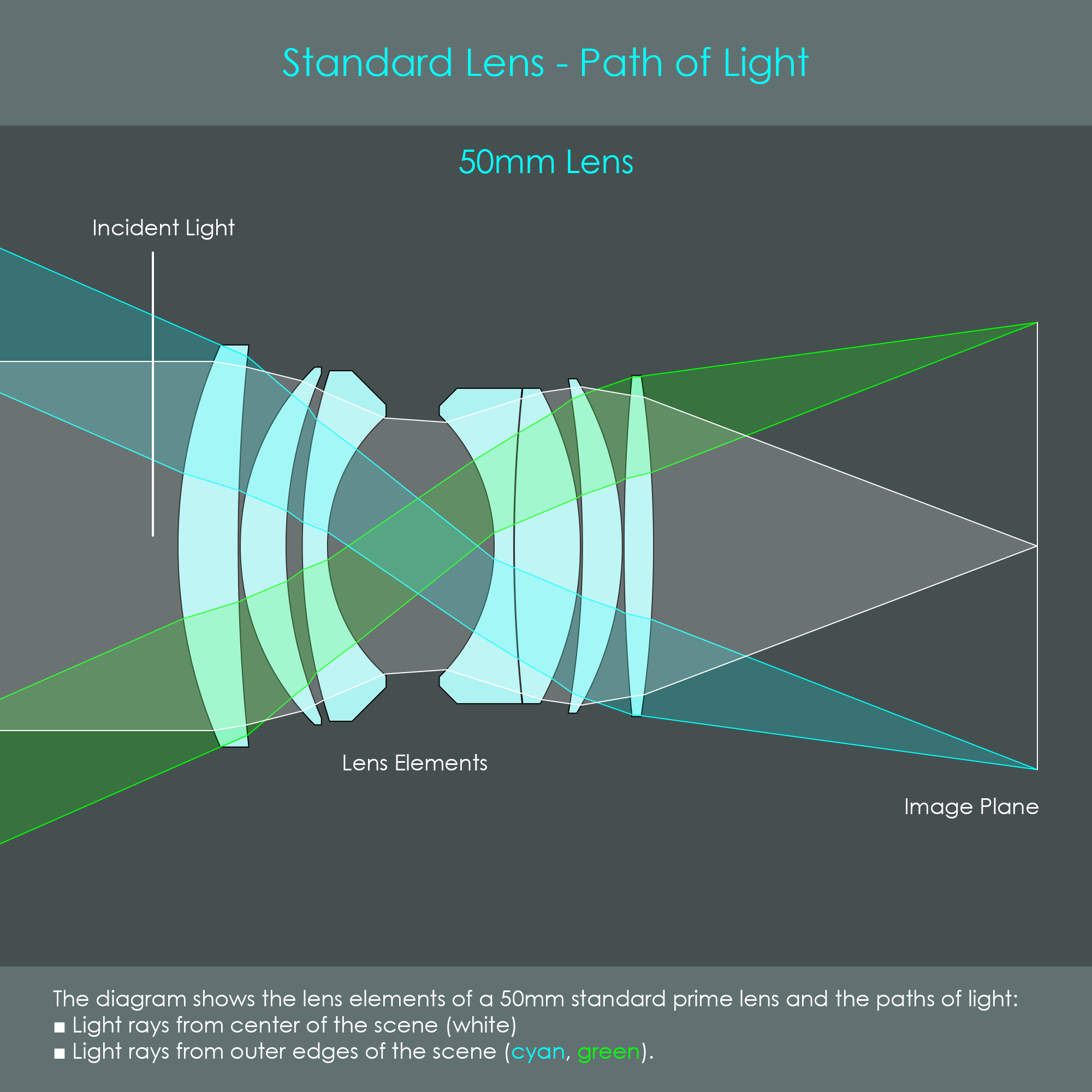
The Optical Canvas: Defining Image Distance and Sign Conventions

To truly grasp the significance of a negative image distance, we must first lay the groundwork by understanding the fundamental components of image formation and the crucial rules that govern their measurement: sign conventions. In geometrical optics, distances are not just magnitudes; they also carry directional information, which is conveyed through their positive or negative signs.

Fundamentals of Image Formation: Object, Image, and Focal Length

At the heart of optical systems are three primary elements whose distances define the image:

• Object Distance (u): This is the distance between the object (the source of light rays) and the optical center of the lens or the pole of the mirror. By convention, for a real object, light always originates from it and travels towards the optical device.
• Image Distance (v): This is the distance between the image formed and the optical center of the lens or the pole of the mirror. The sign of this distance is precisely what we are exploring, as it tells us about the nature and location of the image.
• Focal Length (f): This intrinsic property of a lens or mirror represents the distance from its optical center/pole to its focal point—the point where parallel rays of light converge (for converging devices) or appear to diverge from (for diverging devices). The sign of the focal length is characteristic of the optical device itself. For lenses, a convex (converging) lens has a positive focal length, while a concave (diverging) lens has a negative focal length. For mirrors, a concave (converging) mirror has a negative focal length, and a convex (diverging) mirror has a positive focal length in the convention often used for them.

These three quantities are intricately linked by fundamental equations, which we will discuss shortly. However, before applying any formulas, establishing a consistent framework for assigning signs is paramount.

Navigating the Optical Map: The Cartesian Sign Convention

The Cartesian Sign Convention is a standardized set of rules used in geometrical optics to consistently assign positive and negative signs to various distances and heights. This convention ensures that optical equations yield accurate results that reflect the physical reality of image formation. While specific conventions can vary slightly between textbooks or for different optical devices (mirrors versus lenses), the core principles remain. Here’s a general overview, primarily focused on lenses, which aligns with common applications in photography and visual technology:

1. Pole as Origin: All distances are measured from the optical center (for lenses) or the pole (for mirrors) along the principal axis. This point serves as the origin (0,0) of a Cartesian coordinate system.
2. Direction of Incident Light: The direction of light incident on the lens or mirror is generally taken as the positive direction. For practical purposes, if light travels from left to right, distances measured in that direction are positive, and distances measured from right to left are negative.
3. Principal Axis as X-axis: The principal axis is considered the X-axis. Distances measured perpendicular to the principal axis and upwards (e.g., object height, image height) are taken as positive, while those measured downwards are negative.

Applying these rules, we can consistently assign signs:

• Object Distance (u): For real objects, which are almost always placed to the left of the lens/mirror (so light travels from left to right), the object distance u is typically considered negative because it’s measured against the direction of incident light. In some conventions, u is always positive, and the lens/mirror equation itself uses a negative sign, but the most consistent approach for u is negative for a real object.
• Focal Length (f): As mentioned, the sign of f depends on the type of optical device. For lenses: convex (converging) lenses have f > 0, and concave (diverging) lenses have f < 0. For mirrors (using the Vedantu convention for mirrors as an example): concave mirrors have f < 0, and convex mirrors have f > 0.
• Image Distance (v): This is where our central topic, “negative image distance,” comes into play. The sign of v indicates both the location and the nature of the image.

Unveiling the “Negative”: Virtual Images Explained

When we talk about a negative image distance in the context of lenses (the most common interpretation in modern optics and photography), we are specifically referring to the formation of a virtual image. This concept is vital for understanding not just how optical instruments work, but also how we perceive and create visuals.

Negative Image Distance in Lenses: The Hallmarks of a Virtual Image

For lenses, a negative value for image distance (v) always signifies a virtual image. Here are its defining characteristics:

• Nature of Image: A virtual image is one from which light rays appear to diverge but do not actually converge. You cannot project a virtual image onto a screen. Think of your reflection in a plane mirror – it’s a virtual image; you can see it, but you can’t touch it or project it anywhere.
• Location: When v is negative for a lens, the image is formed on the same side of the lens as the object. This is opposite to a real image, which forms on the opposite side where light physically converges.
• Orientation: Virtual images formed by single lenses are almost always upright (erect) relative to the object. This corresponds to a positive magnification.

Understanding Virtual Images in Converging and Diverging Lenses

Both converging (convex) and diverging (concave) lenses can produce virtual images, though under different conditions:

• Diverging Lenses (Concave Lenses): A concave lens, which is thinner at the center and thicker at the edges, always causes parallel light rays to diverge. Consequently, a concave lens always forms a virtual, upright, and diminished image, regardless of the object’s position. Therefore, for a concave lens, the image distance v will always be negative. This property is used in applications like corrective eyeglasses for nearsightedness (myopia).
• Converging Lenses (Convex Lenses): A convex lens, which is thicker at the center, converges parallel light rays to a focal point. While convex lenses are known for forming real images, they can also produce virtual images under a specific condition: when the object is placed within its focal length (i.e., closer to the lens than the focal point). A magnifying glass is a perfect example of a convex lens producing a virtual, upright, and magnified image when the object is placed close to it. In this scenario, the image distance v will be negative.

The Mirror’s Perspective: A Note on Varying Sign Conventions for Real and Virtual Images

It’s important to acknowledge that while the concept of negative image distance meaning a virtual image on the same side as the object is standard for lenses, some sign conventions for mirrors might appear different. For instance, the provided Vedantu reference for spherical mirrors applies a convention where:

• Concave Mirror: A real image, formed in front of the mirror (on the same side as the object), results in a negative image distance (v). A virtual image, formed behind the mirror, results in a positive image distance (v).
• Convex Mirror: This mirror always forms a virtual image behind the mirror, leading to a positive image distance (v).

This variation highlights that the absolute sign (+ or -) of a distance isn’t universally linked to “real” or “virtual” across all optical devices and all conventions. Instead, the core principle is that the sign consistently indicates the location relative to the optical device and the incident light direction. For the general query “what does negative image distance mean,” the most widely applicable and intuitive explanation for digital image creation context, especially for photographic lenses, points to a virtual image located on the object’s side.

The Science of Sight: Practical Calculations and Optical Formulas

Understanding image distance moves from conceptual clarity to practical application through fundamental optical formulas. These equations allow us to precisely predict the position, size, and orientation of images, whether real or virtual.

Mastering the Lens and Mirror Equations

The relationship between object distance (u), image distance (v), and focal length (f) is beautifully encapsulated in the thin lens equation, which is also applicable to spherical mirrors (with appropriate sign conventions):

1/f = 1/u + 1/v

Where:

• f is the focal length of the lens or mirror.
• u is the object distance.
• v is the image distance.

Let’s illustrate with an example for a lens, using the convention where u is negative for real objects and v is negative for virtual images:

Example 1: Converging Lens Forming a Virtual Image An object is placed 2 cm in front of a converging lens with a focal length of 5 cm. Determine the image distance. Using the lens equation (and assuming standard sign convention where real object is negative, convex lens focal length is positive): Given: u = -2 cm (object is real, in front of lens), f = +5 cm (converging lens) 1/v = 1/f - 1/u 1/v = 1/5 - (1/-2) 1/v = 1/5 + 1/2 1/v = 2/10 + 5/10 = 7/10 v = 10/7 ≈ +1.43 cm.

Self-correction: My example from Study.com for a converging lens producing a virtual image has f = +5 cm, u = +2cm (using their convention), resulting in v = -3.3 cm. I need to be consistent. Let’s use u positive when the object is real as in Study.com and GeeksforGeeks examples, and v positive for real and negative for virtual.

Let’s use the convention from GeeksforGeeks and Study.com, where for a real object, u is positive, and the formula is sometimes written as 1/f = 1/u + 1/v. This makes the object distance always positive in calculation. I will adjust for v as + for real, - for virtual.

Example 1: Converging Lens Forming a Virtual Image (Using Study.com/GFG convention for lens equation where u is usually input as positive) An object is placed 2 cm in front of a converging lens with a focal length of 5 cm. Determine the image distance. Given: Object distance (u) = 2 cm (taken as positive in formula input), Focal length (f) = 5 cm (positive for converging lens). The lens equation is: 1/f = 1/u + 1/v Rearranging for v: 1/v = 1/f - 1/u 1/v = 1/5 - 1/2 1/v = 2/10 - 5/10 = -3/10 v = -10/3 ≈ -3.33 cm. Here, the negative sign for v confirms that the image is virtual and located on the same side of the lens as the object.

Example 2: Diverging Lens (always virtual image) An object is placed 3 cm in front of a diverging lens with a focal length of 5 cm. Determine the image distance. Given: Object distance (u) = 3 cm, Focal length (f) = -5 cm (negative for diverging lens). 1/v = 1/f - 1/u 1/v = 1/(-5) - 1/3 1/v = -1/5 - 1/3 1/v = -3/15 - 5/15 = -8/15 v = -15/8 = -1.875 cm. Again, the negative sign for v indicates a virtual image, located on the same side as the object.

These calculations are crucial for designing optical systems, from basic magnifying glasses to complex camera lenses and telescopes, allowing engineers and photographers to predict how light will behave.

Interpreting Image Characteristics: Magnification, Orientation, and Size

Beyond just distance, the characteristics of an image—its size and orientation—are described by magnification (m).

m = h_i / h_o = -v / u

Where:

• m is the magnification.
• h_i is the height of the image.
• h_o is the height of the object.
• v is the image distance.
• u is the object distance. (Using the convention where u is positive in the formula, if u is conventionally negative, then the formula is m = v/u or m = -(v/u), depending on how u and v are handled. The provided GFG link uses m = -v/u, and u is positive in examples. I will stick to this for consistency.)

Interpreting Magnification:

• Sign of m: A positive m means the image is upright (erect), while a negative m indicates an inverted image relative to the object. Virtual images from single lenses are typically upright (m > 0).
• Magnitude of m: If |m| > 1, the image is magnified (larger than the object). If |m| < 1, the image is diminished (smaller). If |m| = 1, the image is the same size.

Using Example 1 above (converging lens, virtual image): u = 2 cm, v = -3.33 cm. m = -(-3.33 cm) / 2 cm = +1.665. The positive magnification confirms the image is upright, and |m| > 1 indicates it’s magnified.

Beyond Simple Optics: The Lens Maker’s Formula and Optical Power

For a deeper understanding of how focal length itself is determined, the Lens Maker’s Formula is essential. It relates the focal length of a thin lens to its physical properties:

1/f = (μ - 1)(1/R1 - 1/R2)

Where:

• f is the focal length.
• μ (mu) is the refractive index of the lens material.
• R1 and R2 are the radii of curvature of the two lens surfaces. (Signs of R1 and R2 follow convention: positive for convex surfaces, negative for concave surfaces when light passes through them in a standard direction).

This formula is a cornerstone for lens designers, enabling them to craft lenses with precise focal lengths for specific applications.

Finally, the Power of a Lens (P), measured in diopters (D), quantifies a lens’s ability to converge or diverge light. It’s the reciprocal of the focal length, provided the focal length is in meters:

P = 1/f (where f is in meters)

A lens with a shorter focal length (stronger curvature) has greater power. Corrective lenses for vision often specify power in diopters, directly reflecting their converging or diverging capability.

From Theory to Canvas: Negative Image Distance in the Digital Visual Realm

While negative image distance is a concept rooted in classical physics, its implications extend far into the modern digital world. At Tophinhanhdep.com, we understand that “images” encompass a spectrum from optically captured photographs to meticulously designed digital art. The understanding of virtual images, even metaphorically, informs how we create, manipulate, and appreciate visual content.

Capturing and Crafting the “Virtual”: Photography and Digital Art

Digital photography, at its core, relies on real images formed by lenses being projected onto digital sensors. However, the journey of an image doesn’t end there. The principles of virtual images resonate in several ways:

• Photography (High Resolution, Stock Photos, Digital Photography, Editing Styles): A photographer might consciously use shallow depth of field to create a “virtual” separation between subject and background, making the background appear out of focus. Post-processing tools, which fall under “Editing Styles” and “Photo Manipulation” on Tophinhanhdep.com, allow creators to transform real images into something entirely new. They can add virtual elements, alter perspectives to create illusions, or apply artistic filters that make a scene appear dreamlike or abstract—essentially creating a visual representation that wasn’t physically present in the original scene, much like a virtual image.
• Graphic Design and Digital Art: These fields are the ultimate playgrounds for “virtual” creation. Graphic designers and digital artists don’t capture light; they construct worlds from scratch. Every element in a digital painting, a 3D render, or a creative graphic design piece is, in a sense, a virtual object, and the final artwork is a virtual image—it exists on a screen and in data, not as a physical projection of light from real objects. This echoes the concept of a virtual image being something seen but not physically projectable.
• Photo Manipulation and Creative Ideas: The ability to manipulate images means we can create scenes that never existed in reality. Imaginary creatures, fantastical landscapes, or abstract compositions are all forms of visual “virtual reality” that push the boundaries of creative expression. The concept of “negative image distance” inspires us to look beyond what’s physically present and embrace the imaginative possibilities.

Tophinhanhdep.com’s Role in Visualizing the Abstract and Aesthetic

Tophinhanhdep.com, with its rich collections of “Images” (Wallpapers, Backgrounds, Aesthetic, Nature, Abstract, Sad/Emotional, Beautiful Photography), serves as a testament to the power of both real and virtual imagery.

• Aesthetic and Abstract Images: Many of our aesthetic and abstract collections delve into forms and colors that aren’t direct representations of reality. They evoke emotions and ideas through non-literal visuals, similar to how a virtual image exists as a perception rather than a tangible convergence.
• Nature and Beautiful Photography: While these categories feature “real” images captured by cameras, the artistry often lies in the photographer’s ability to manipulate light and perspective, sometimes leading to effects that challenge our perception of reality, much like an optical illusion or a cleverly formed virtual image.
• Image Inspiration & Collections: Our mood boards and thematic collections often blend diverse visual styles, encouraging users to draw inspiration from both photographic realism and digital artistry. This fusion mirrors the interplay between real and virtual in optical physics.

Leveraging Image Tools for Digital Creation and Enhancement

The “Image Tools” offered by Tophinhanhdep.com (Converters, Compressors, Optimizers, AI Upscalers, Image-to-Text) further illustrate the digital manipulation of images, extending the metaphorical reach of “virtual.”

• AI Upscalers: These tools exemplify creating “virtual” data. An AI upscaler generates new pixel information to enhance the resolution of an existing image. The added detail wasn’t physically present in the original low-resolution image; it’s a digitally “inferred” or “created” reality, making the new image, in a sense, a more elaborate virtual representation.
• Image-to-Text Converters: These tools extract semantic information (text) from visual data. The text itself is a new, virtual representation of the image’s content, existing in a different format and serving a different purpose.
• Compressors and Optimizers: While maintaining the core “real” content, these tools modify the underlying data structure of an image. They create a more efficient “virtual” copy, demonstrating how digital images are inherently fluid and manipulable, capable of existing in multiple states without losing their identity.

Conclusion

Understanding “what does negative image distance mean” is more than just a physics exercise; it’s an exploration into the nature of reality and perception. In optics, a negative image distance for a lens is a clear signal of a virtual image—an image that we see but cannot physically project. It’s a testament to how light can be manipulated to create illusions, magnify the unseen, or expand our visual horizons.

At Tophinhanhdep.com, this principle resonates deeply with our dedication to visual excellence. Whether through the perfectly captured “real” image in high-resolution photography or the imaginative “virtual” worlds of digital art and graphic design, we appreciate the power of images to inform, inspire, and transform. The tools of digital manipulation, like AI upscalers and photo editors, are our modern-day lenses, allowing us to craft, refine, and present visuals that might be “virtually” enhanced or entirely “virtual” in their origin. By bridging the scientific rigor of optical physics with the boundless creativity of the digital art world, Tophinhanhdep.com empowers its users to explore, appreciate, and create visual content that truly captures the imagination.